It is interesting to know how to change the coordinates of a point in one coordinate system and the respective new coordinates of the same pont in a new coordinate system. The immediate application can be just the graphic representation of a point given by its coordinates in an oblique coordinate system converted to the cartesian coordinates of the computer screen. In this page one system is cartesian and the other system is oblique where the x and y axes in the oblique system are the same as in the cartesian system and the z axis is also perpendicular to the y axis but its intersection on  x axis shows the angle  in the range 180^o>>90^o.
The observation of the above animated graphic boards numbered from 1 to 28 and the respective cartesian coordinates of the polihedral vertices is an intruduction to this study.

Each graphic board shows a parallel projection of a parallelepiped vith vertices numbered with even numbers from [0] to [6] on the cartesian xy plane. Vertex [0] is the origin of the cartesian coordinate system, the cartesian x axis intersects vertex [2] and the cartesian axis y intersects vertex [6]. Vertices numbered with odd numbers from [1] to [7] define a plane parallel to xy, vertex [1] belongs to cartesian plane xz and the  angle of the segment [1]-[0] with the x axis is in the range 180^o>>90^o. The cartesian coordinates of all vertices are presented in blue and in arbitrary units on all graphic boards.

The parallel projection on graphic board 2 results after the parallelepiped and the base on graphic board 1 was rotated 18 degrees about the cartesian axis x and graphic board 3 after next 18 degrees of rotation and so on until graphic board 21 returns the same as graphic board 1. Graphic board 22 shows the cpmplete set rotated 5 degrees about the diagonal defined by vertices [0] and [5] of the parallelepiped, graphic board 23 after next 5 degrees and so on until graphic board 28. this page can be reloaded so many times as necessary until the observed and repeated details are recognized and the whole meaning is reached.
A useful frame may be a straw parallelepiped, mounted with straw, threaded by cotton twine, tied with knots. The frame can be upgraded with numbers labeled with any overhead projector pen, according to the sequence on the graphic board vertices.

Questions
1) What is the number of the graphic board where the correct  angle in the range 180^o>>90^o. can be measured directly on the computer screen with a protractor?
2) Find the correct  angle using the dot product of vectors defined by the coordinates of the vertices on the boundaries of the proper edges and compare with the value measured with the protractor, by the way: is the computer screen close to sqare or very rectangular?

Second section
 Figure-1 presents a pink oblique  parallelepiped in perspective wit point P on vertex with all coordinates greater than zero on a cartesian x, y and z coordinate system and on an oblique referential defined by axis x, y and by the third axis, see table-1, whith intersections on vertices p_oz and O. The x axis of the oblique coordinate system intersects vertices O and p_ox and the y axis intersects vertices O and p_oy. The third axis of the oblique coordinate system is perpendicular to y axis and intersects the x axis at angle  in the range 180^o>>90^o. The coordinate p_oy of point P on the oblique system has the same vallue as the coordinate p_cy of point P on the cartesian system, as can be observed on figure-1 and as defined on table-1. The straight line parallel to axis x  intersects vertices p_oz and n also intersects axis z at point p_cz.

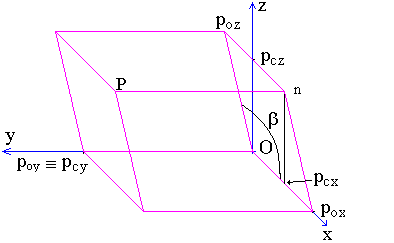
Figure-1. Coordinates of point P in cartesian and oblique coordinate systems.

Tabel-1. Coordinates of point P on the first, second and third axis.

Coordinate system	Coordinates on the first axis	Coordinates on the second axis	Coordinates on the third axis
Oblique, 180o>>90o.	pox	poy  , (poy  = pcy)	poz
Cartesian	pcx	pcy  , (pcy = poy)	pcz

As shown in figure-1, triangle p_oz, p_cz and O and triangle p_ox, p_cx and n have parallel edges and are equal because the points O, p_cz, n and p_cx define a rectangle.
It is important  to note that segment p_oz - p_cz is equal to segment p_cx - p_ox.

Now the coordinates of point P in the cartesian coordinate system can be calculated from the coordinates of point P in the oblique coordinate system.

p_cx = p_ox + [p_oz * cos(  )]

p_cy = p_oy

p_cz = p_oz * sin(  )

More questions

3) What is the value  of the coordinates of vertex [5] of the parallelepiped presented on graphic board 28 considering the oblique coordinate system?
4) The coordinates of vertex [5] on the parallelepiped on graphic board 1 considering the oblique coordinate system are different of those obtained on question 3)? Justify.

Please send your comments.

Table of subjects.

Presentation
Other	Varied	Oblique and orthogonal systems study
		Diary
		Study of the oblique at all coordinate system and the orthogonal coordinate system
		The Great Wall of China and the Great Higway of Love