Numa das páginas mais antigas foi apresentado o Estudo do Referencial Oblíquo e Ortogonal, aquele referencial oblíquo é caracterizado pelo ângulo  90^o<  <180^o. maior do que 90^o entre o primeiro e terceiro eixo referencial.
Aqui se estuda a obtenção das coordenadas de um ponto P num referencial ortogonal a partir das coordenadas do mesmo ponto P num "referencial oblíquo em todos os ângulos", ROTA, no qual os 3 ângulos entre os eixos referenciais, ,  e  são diferentes de 90^o e diferentes entre si.

Para iniciar o estudo posiciona-se a origem do referenciail ortogonal no mesmo ponto de origem do ROTA e o primeiro eixo do referencial ortogonal coincide com o primeiro eixo do outro referencial, assim como o plano que contém o primeiro e o segundo eixo do referencial ortogonal coincide com o plano dos dois primeiros eixos do ROTA.
A tabela-1 apresenta detalhes da sequência de pranchas mostradas na animação acima sobre o estudo das coordenadas Pu, Pv e Pw do ponto P em referencial ortogonal obtidas a partir das coordenadas PX, PY e PZ do mesmo ponto no ROTA. Todos os desenhos das pranchas são projeções paralelas onde o número de 1 a 398 pode ser observado no topo de cada prancha, respectivamente. Para tornar a observar uma prancha é preciso recarregar a página.

Tabela-1. Detalhes do estudo das coordenadas do ponto P no "referencial oblíquo em todos os ângulos" e no referencial ortogonal.

Projeção paralela	Outra projeção paralela	Detalhes das projeções
1	6	Mostra o ponto P no ROTA definido pelo paralelepípedo em vermelho e em azul no referencial ortogonal. As mesmas cores serão utilizadas em todas as imagens, respectivamente. Ambos os referencias compartilham: a mesma origem no ponto 0 o primeiro eixo referencial que intercepta os pontos 0, 2, e 8 o mesmo plano em amarelo que intercepta os pontos: 0, 2, 4, 6, 8, 9 e 12.
2	7	Mostra o ponto P apenas no ROTA definido pelo paralelepípedo com as arestas em cinza encobertas.
3	8	Mostra os eixos referencias X, Y e Z no ROTA em preto, assinalados na extremidade positiva de cada eixo e os parâmetros das coordenadas PX, PY e PZ e dos ângulos: alfa abreviado como al, localizado entre os eixos Z e Y, beta, abreviadobe, entre eixos X e Z e gama, abreviado ga entre X e Y em verde. Mostra as diagonais: f1, do ponto 1 sobre Z ao ponto 2 sobre X f2, do ponto 6 zobre Y ao ponto 1 sobre Z.
4	9	Mostra o ponto P apenas no referencial ortogonal definido pelo paralelepípedo com as arestas em cinza encobertas.
5	10	Mostra os referenciais u, v e w em preto, assinalados na extremidade positiva de cada eixo ortogonal. Mostra também os parâmetros das coordenadas do ponto P: Pu, Pv e Pw em verde.
	11	Mostra o ponto P nos dois referenciais antes das rotações.
	398	Mostra o alinhamento final após 387 etapas de rotação. Os pontos P, 7 e 11 estão alinhados sobre a mesma reta suporte perpendicular à tela do computador e o ponto P está superposto aos outros dois. Mostra a aresta vermelha horizontal 3_P no fundo da prancha que encobre parcialmente a aresta 13_P azul do referencial ortogonal. Mostra a aresta do referencial ortogonal 8_12, horizontal azul no topo da prancha que encobre também a aresta 2_4, vermelha do ROTA.

A seguir aresenta-se a construção das equações que definem as coordenadas do ponto P no referencial ortogonal a partir das coordenadas do mesmo ponto P no ROTA. O método denominado "Trilateration", descrito também na página da internet da Wikipedia, foi  utilizado até as equações [5] e [9], para obter as coordenadas ortogonais do ponto 1, vide pranchas de 1 a 3 da animação. Numa etapa posterior, a partir das coordenadas ortogonais do ponto 1 chega-se às coordenadas ortogonais do ponto P, apresentadas nas equações [15], [18] e [21]. Os desenhos das animações e o da figura-1 estão na mesma escala. A figura-1 (a) apresenta as 3 esferas do procedimento "trilateration",  centradas no plano comum que contém os dois primeiros eixos do ROTA e os dois primeiros eixos do  referencial ortogonal. Observa-se na figura 1 (a) e (b) a aresta 0_2, de comprimento PX. Esta aresta PX será denominada simplesmente a na dedução das coordenadas do ponto P no referencial ortogonal apresentada abaixo. Também o raio da esfera centrada em 0, com comprimento PZ na figura-1 (a) e a aresta 0_1 desenhada na  figura-1 (b) e (c)  será denominada c. E e a aresta 0_6, de comprimento PY na figura-1 (a) e figura-1 (c) será denominada b. A projeção paralela do ponto P no plano dos dois primeiros eixos do referencial ortogonal , Puv é assinalada pela cruz em vermelho na figura-1 (a). A figura-1 (b) mostra como calcular o comprimento da diagonal f1 e a figura-1 (c) ilustra o cálculo do comprimento da diagonal f2.
 

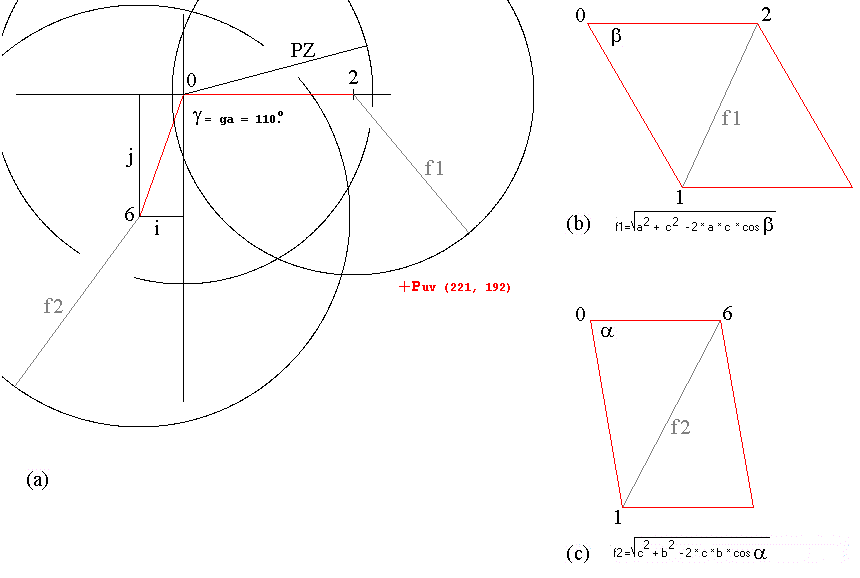
Figura-1. (a) = Desenho que ilustra o cálculo "trilateration" em escala igual aos desenhos das pranchas animadas. (b) Desenho em escala igual ao das pranchas animadas que ilusta o cálculo da diagonal f1. (c) Desenho em escala igual ao das pranchas animadas que ilusta o cálculo da diagonal f2, isto será encontrado em qualquer bom livro básico de trigonometria.

Na seção abaixo apresenta-se a obtenção das coordenadas do ponto P abreviadas como  u, v e w no referencial ortogonal a partir das coordenadas do mesmo ponto P no outro referencial. A interseção das 3 esferas representadas na figura-1 (a) será calculada até a equação [9], para converter preliminarmente as coordenadas do ponto 1 do paralelepípedo apresentado nas pranchas 3 e 8 para as coordenadas cartesianas do ponto 1 observado nas pranchas gráficas 5 e 10.
Utiliza-se a equação [1] da esfera centrada em 0 na figura-1 (a), lembrando que a coordenada PZ é representada pelo parâmetro c:

 c² = x² + y² + z²         [1]

Utiliza-se a equação da próxima esfera, centrada em 2 na figura-1 (a).

( f1 )² = ( x - a )² + y²  + z²     [2]

Utiliza-se também a equação da esfera centrada no ponto 6 da figura-1 (a). As equações que definem i e j serão utlizadas mais adiante, em [11] e [12].

( f2 )² = ( x - i )² + ( y - j )² + z²      [3]

A condição abaixo sempre será satisfeita no paralelepípedo definido pelo ponto P no ROTA.

( a - c ) < f1 < ( a + c )     [4]

obtenção de x, [1] - [2]:

x = ( c ² - f1² +  a² ) / ( 2 * a )      [5]

A equação [5] fornece a primeira coordenada ortogonal do ponto 1 do paralelepípedo apresentado na prancha 5 e 10.

Após substituição de [5] em [1]:

 ( c )²  = {[c² - f1² + a² ]² / 4a² } + y² + z²       [6]

Com o rearranjo de [1]:

y² + z² = c ² - x²        [7]

substituição de [7] em [3] e após simplificar:

( f2 )² =( i*2 ) - ( 2 * x * i ) + (2 * j) -( 2 * y * j ) + c²             [8]

após rearranjo para isolar y:

y = [ c² - ( f2 )² + i² + j² - ( 2 * x * i ) ] / (  2 * j )        [9]

A equação [9] fornece a segunda coordenada ortogonal do ponto 1 do paralelepípedo estudado na prancha 5 e 10.

Para obter a primeira coordenada ortogonal u, do ponto P no referencial ortogonal :

u = a + i + x               [10]

lembrar:

i = b * cos             [11]

j = b * sen             [12]

f1 = ( a² + c² - 2 * a * c*cos  )^0.5                       [13]

f2 = (c² + b² - 2 * c * b*cos  )^0.5                       [14]

substituição de [5] e [11]  e [13] em [10] e rearranjo para obter a coordenada u do ponto P no referencial ortogonal:
 

u = a + ( b  * cos ) + ( c * cos )                        [15]

de [15] e [10] pode-se concluir:

x = c * cos                [16]

Para calcular a segunda coordenada v:

v = j + y                [17]

substituição de [9] e [11] e [12] e [14] e [16] em [17] para obter a coordenada v do ponto P no referencial ortogonal:
 

v = ( b  * sen ) + [ c * (cos - cos * cos ) / sen]                      [18]

cálculo da coordenada w do ponto P no referencial ortogonal:

lembrar:

volume do paralelepípedo totalmente oblíquo, vide prancha 3, 8 e outras, favor notar que a=PX, b=PY e c=PZ:

volume =  a * b * c * [1-cos²() - cos²() - cos²() + 2 * cos * cos * cos ]^0.5            [19]

cálculo da área da base (ab) do paralelepípedo totalmente oblíquo:

lembrar: volume do paralelepípedo também é igual ao produto da área da base pela altura

área da base (ab) = a * b * sen                         [20]

a coordenada w procurada é a própria altura do paralelepípedo totalmente oblíquo, obtida pela divisão [19] / [20]:
 

w = { c * [1-cos2() - cos2() - cos2() + 2 * cos * cos * cos ]0.5 }/ sen                           [21]

Este procedimento foi utilizado no aplicativo GIRA7B.

Exercício

Deduzir as coordenadas dos pontos 0, 1, 2, ...P, ... 7  e transferir estas coordenadas no ROTA para o aplicativo GIRA7B e identificar a projeção paralela do paralelepípedo vermelho existente na prancha 398. Apresentar os valores das coordenadas ortogonais do ponto P obtidas nas páginas azuis do aplicativo GIRA7B e escrever o que deve ser realizado para encontrar a projeção solicitada, em branco e preto. Concluir.

Por favor, envie teus comentários.

Tabela de temas.

Apresentação
Outro	Variado	A Grande Muralha da China e a Grande Rodovia do Amor
		Agenda de bolso
		Assis, aciz, zica
		Estudo do referencial oblíquo e ortogonal
		Estudo do referencial totalmente oblíquo e do referencial ortogonal
		O Pai, o Céu, a Terra e nos
		Pequena história da teleeducação
		Regressão linear e estatística