En malnova pagxo oni prezentis “Studo de oblikva kaj orta referencialo”. Cxi tiu referencialo oblikva estas karakterizita de ângulo 90o <  < 180o, pli granda ol 90^o inter la unua kaj la tria referenca akso.
Oni studas la akiron de la koordinatoj de la punkto P en orta referencialo komence de la koordinatoj de la sama punkto en “oblikva referencialo en cxiuj anguloj”, ORCA, en kiu la 3 anguloj inter la referencaj aksoj, ,  e  estas malsamaj de 90^o kaj malsamaj inter ili.

Inicante la studon oni lokas la originon de la orta referencialo en la origina punkto de ORCA, kaj la unua akso de la orta referencialo koincidas kun cxi tiu kiu entenas la unuan kaj la duan akson de la orta referencialo koincidas kun la plano de la du unuaj aksoj de ORCA. La  tabelo-1 prezentas detalojn de la sekvenco de tabuloj montritaj en la movigxado cxi supre montrita, tra la studo de la koordinatoj Pu, Pv kaj Pw de la punkto P en orta referencialo akiritaj komence de la koordinatoj PX, PY kaj PZ de la sama punkto en ORCA. Cxiuj desegnoj de la tabuloj estas paralelaj projekcioj kie la numeroj 1 gxis 398 povas esti viditaj supre de la tabelo koncerna. Por, denove, rigardi la koncernan tabulon oni bezonas rekomenci la movigxadon.

TABELO-1. Detaloj de la studo de la koordinatoj de la punkto P en la “referencialo oblikva en ciuj anguloj” kaj en la orta referencialo.

Paralela projekcio	Alia paralela projekcio	Detaloj de la projekcio
1	6	Montras la punkton P en ORCA difinita pere de paralelepipedo, rugxe, kaj blue, en la orta referencialo. La samaj koloroj estas uzitas en cxiuj figuroj, respektive. Ambaux referencialoj havas kune: la saman originon punkton 0 la unuan referencan akson kiu trapasxas la punktojn 0, 2 kaj 8 la saman planon, flave, kiu trapasxas la punktojn 0,2, 4, 6, 8, 9 kaj 12.
2	7	Montras la punkton P nur en ORCA, difinitan de la paralelepipedo kun la egxoj cindre desegnitaj.
3	8	Montras la refencajn aksojn X, Y kaj Z en ORCA, nigre desegnitajn en la ekstremo pozitiva de cxiu akxo kaj la parametrojn de la koordinatoj PX, PY kaj PZ kaj de la anguloj: alfa (mallongita al), lokitan inter la aksoj Z kaj Y, beta (mallongita be) inter la aksoj X kaj Z kaj gama (mallongita ga) inter la aksoj X kaj Y, verde. Montras la diagonalojn: f1, de la punkto 1 sur Z gxis la punkto 2 sur X f2, de la punkto 6 sur Y gxis la punkto 1 sur Z.
4	9	Montras la punkton P nur en la orta referencialo difinita de la paralelepipedo kun la egxoj cindre desegnitaj.
5	10	Montras la referencajn u, v kaj w, nigre desegnitajn en la pozitiva ekstremo de cxiu orta akso. Ankaux montras la parametrojn de la koordinatoj de la punkto P: Pu, Pv kaj Pw, verde.
	11	Mostra o ponto P nos dois referenciais antes das rotações.
	398	Montras la finan rektliniigon post 387 rotacioj. La punktoj P, 7 kaj 11 estas liniigitaj sur la sama rekto orte la komputila ekrano, kaj la punkto P estas surmetigxita al la du aliaj. Montras la rugxan egxon horizontalan 3_P ene de la tabulo kiu kasxkovras, parte, la egxon 13_P, blue, de la orta referencialo. Montras la egxon de la orta referencialo 8_12 horizontala, blue, en la supro de la tabulo kiu kasxkovras ankaux la egxon 2_4, rugxe, en la ORCA.

Sekve oni prezentas la konstruadon de ekvacioj kiuj difinas la koordinatojn de la punkto P en la orta referencialo ekde la koordinatoj de la sama punkto P en ORCA. La metodo nomita “Trilateration” montrita ankaux en la interrekta pagxo de Wikipedia, estis uzita gxis la ekvacioj [5] kaj [9], por havigi la ortajn koordinatojn de la punkto 1, vidu tabulojn 1 gxis 3 de la movigxado. En posta etapo, komence de la ortaj koordinatoj de la punkto 1 oni atingas la ortajn koordinatojn de la punkto P, prezentitajn tra la ekvacioj [15], [18] kaj [21]. La desegnoj de la movigxadoj kaj de la Figuro-1 estas en la sama skalo. La figuro-1 (a) prezentas la 3 sferojn de la procedo “Trilateration”, centritajn en sama plano kiu entenas la du unuajn aksojn de ORCA kaj la du unuaj aksoj de orta referencialo. Observu en la Figuro-1 (a) kaj (b) la egxo 0_2, kies longo esta PX. La egxo PX estas nomita simple a en la dedukto de la koordinatoj de la punkto P en la orta referencialo prezentita cxi sube. Ankaux la sfera radiuso centrita en 0, kies longo estas PZ, sur la Figuro-1 (a) kaj Figuro-1 (c) estas nomita c. Kaj observu en la Figuro-1 (a) kaj (b) la egxo 0_6, kies longo esta PY. La egxo PX estas nomita simple b.
La projekcio paralela de la punkto P en la plano de la du unuaj aksoj de orta referencialo, Puv estas signalita de la kruco, rugxe, sur la Figuro-1 (a). La Figuro-1 (b) montras kiel kalkuli la longon de la diagonalo f1, kaj la Figuro-1 (c) montras kiel kalkuli la longon de la diagonalo f2.

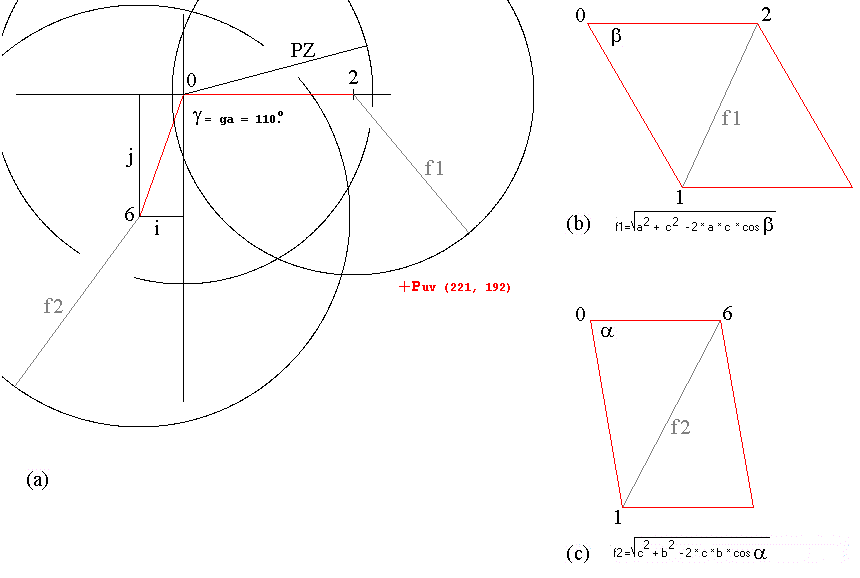
Figuro-1 (a) Desegno kiu montras la kalkulon “Trilateration” en egala skalo de la desegnoj de movigxadaj tabuloj. (b) Desegno en egala skalo de la movigxadaj tabuloj kiu montras la kalkulon de la diagonalo f1. (c) Desegno en egala skalo de la movigxadaj tabuloj kiu montras la kalkulon de la diagonalo f2, kion oni trovas en iu ajn baza trigonometria libro.

En la suba sekcio oni prezentas la akiron de la koordinatoj de la punkto P, mallongitaj kiel u, v kaj w en la orta referencialo komence de la koordinatoj de la sama punkto P en la alia referencialo. La interkrucigo de la 3 sferoj prezentitaj en la Figuro-1 (a) estos kalkulita gxis la ekvacio [9], por unue sxangxi la koordinatojn de la punkto 1 de la paralelepipedo prezentita sur la tabuloj 3 kaj 8 por la karteziaj koordinatoj de la punkto 1 montritaj sur la tabuloj 5 kaj 10.

Oni uzas la ekvacion [1] de la sfero centrita en 0 sur la figuro-1 (a). Memorigu ke la koordinato PZ estas reprezentita de la parametro c:

 c² = x² + y² + z²         [1]

Oni uzas la ekvacion de la alia sfero, centrita en 2 sur la Figuro-1 (a).

( f1 )² = ( x - a )² + y²  + z²     [2]

Oni uzas ankaux la ekvacion de la sfero centrita en la punkto 6 sur la Figuro-1 (a). La ekvacioj kiuj difinas i kaj j, estos uzitaj poste, en [11] kaj [12].

( f2 )² = ( x - i )² + ( y - j )² + z²      [3]

La suba kondicxo cxiam validas en la paralelepipedo difinita de la punkto P en ORCA.

( a - c ) < f1 < ( a + c )     [4]

Havigo de x, [1] – [2]:

x = ( c ² - f1² +  a² ) / ( 2 * a )      [5]

La ekvacio [5] produktas la unuan ortan koordinaton de la punkto 1 de la paralelepipedo prezentita en la tabulo 5 kaj 10.

Post anstatauxigo de [5] en [1]:

 ( c )²  = {[c² - f1² + a² ]² / 4a² } + y² + z²       [6]

Com o rearranjo de [1]:

y² + z² = c ² - x²        [7]

Anstatauxigo de [7] en [3] kaj simpligante:

( f2 )² =( i*2 ) - ( 2 * x * i ) + (2 * j) -( 2 * y * j ) + c²             [8]

Post rearangxi por havigi y:

y = [ c² - ( f2 )² + i² + j² - ( 2 * x * i ) ] / (  2 * j )        [9]

La ekvacio [9] liveras la duan ortan koordinaton de la punkto 1 de la paralelepipedo montrita en tabuloj 5 kaj 10.

 Por havigi la unuan ortan koordinaton u de la punkto P en la orta referencialo:

u = a + i + x               [10]

Memorigu:

i = b * cos             [11]

j = b * sen             [12]

f1 = ( a² + c² - 2 * a * c*cos  )^0.5                       [13]

f2 = (c² + b² - 2 * c * b*cos  )^0.5                       [14]

Anstatauxigo de [5] kaj [11] kaj [13 en [10], rearangxo por produkti la koordinaton u de la punkto P en la orta referencialo:
 

u = a + ( b  * cos ) + ( c * cos )                        [15]

Ekde [15] kaj [10] oni konkludas:

x = c * cos                [16]

Por kalkuli la duan koordinaton v:

v = j + y                [17]

Anstatauxigo de [9] kaj [11] kaj [12] kaj [14] kaj [16] en [17] por liveri la koordinaton v de la [punkto P en orta referencialo:
 

v = ( b  * sen ) + [ c * (cos - cos * cos ) / sen]                      [18]

Kalkulo de la koordinato w de la punkto P en la orta referencialo

Memorigu::

Volumeno de la paralelepipedo tute oblikva, vidu tabulon 3, 8 kaj aliajn. Bonvolu observi a=PX, b=PY kaj c=PZ:

volumeno =  a * b * c * [1-cos²() - cos²() - cos²() + 2 * cos * cos * cos ]^0.5            [19]

Kalkulo de areo de bazo (ab) de la paralelepipedo tute oblikva:

Memorigu: volumeno de la paralelepipedo egalas la produton de la baza areo kaj la alto.

Baza areo (ab)  = a * b * sen                         [20]

La koordinato w dezirita estas la alto de la paralelepipedo tute oblikva, havigita de la divido  [19] / [20]:
 

w = { c * [1-cos2() - cos2() - cos2() + 2 * cos * cos * cos ]0.5 }/ sen                           [21]

Cxi tiu procedo estis uzita en aplikfiguro  GIRA7B.

Ekzerco

DKalkuli la koordinatojn de la punktoj 0, 1, 2, …., P, …., 7 kaj transporti cxi tiujn koordinatojn de la ORCA al la aplikfiguro GIRA7B kaj montri la paralelan projekcion de la rugxa paralelepipedo en la tabulo 398. Montri la valorojn de ortaj koordinatoj de la punkto P, kalkulitaj en la bluaj pagxoj de la aplikfiguro GIRA7B kaj skribi kion oni devas fari por havi la deziritan projekcion blank-nigra. Konkludi.

Bonvolu sendi viajn komentariojn.

Tabelo de Temoj

Prezento
Alia	Variita	La Granda Murego de Cxinio kaj la Granda Sxoseo de la Amo
		Posxagendo
		Studo de la oblikva kaj orta referencialo
		Studo de referencialo tute oblikva kaj de orta referencialo