In one of the previous pages the study of the oblique coordinate system and orthogonal coordinate system was presented and the oblique coordinate system was characterized with , the angle between the first and the third coordinate axis such that 90^o<  <180^o.

How to obtain the orthogonal coordinates of point P when the coordinates of point P are given in a total oblique system where the intersctions ,  and  of the coordinate axes are not mutually orthogonal, CANMO, is discussed in this section.

Initially set the origin of the orthogonal coordinate system and the CANMO origin coincident and the first axis of the orthogonal coordinate system coincident with  the first axis of the  CANMO and also the plane defined by the first two orthogonal coordinates coincident with the plane defined by the first and second CANMO.

Table-1 presents details on the sequence of graphic boards showed on the above animation directed to the study of orthogonal coordinates Pu, Pv and Pw derived from PX, PY and PZ of the same point P on CANMO. All the drawings on the graphic boards are parallel projections where the number 1 to 398 can be observed on the top of each graphic board, respectively. To replay a graphic board it is necessary to reload the page.

Table-1. Details of the study of coordinates of point P in orthogonal coordinates and not mutually orthogonal coordinates.

Parallel projection	Other parallel projection	Details of the projections
1	6	Shows point P on CANMO defined by the red parallelepiped and in blue on the orthogonal. Tha same color system is true for all the images in this page. Both coordinate systems share:  the same origin on point 0 the same first coordinate axis intercepting points 0, 2 and 8 the same plane in yellow that intercepts points: 0, 2, 4, 6, 8, 9 and 12.
2	7	Shows point P only on CANMO defined by the parallelepiped with hidden edges in gray.
3	8	Shows X, Y and Z CANMO in black on the positive side and the parameters PX, PY and PZ and the angles alpha, in short al, between Z and Y axes, beta, in short be, between axes X and Z and gamma, in short ga, between X and Y in green. Shows the diagonals:  f1, from point 1 on Z to point 2 on X f2, from point 6 on Y to point 1 on Z.
4	9	Shows point P only on the orthogonal system defined by the parallelepiped with hidden edges in gray.
5	10	Shows coordinate axes u, v and w in black on the positive side. Shows the orthogonal coordinate parameters of point  P: Pu, Pv and Pw in green.
	11	Shows point P on both coordinete systems before rotations.
	398	Shows final alignment after 387 rotation steps. Points P, 7 and 11 are on the same line perpendicular to the screen with point P on covering points 7 and 11. Shows the red horizontal edge 3_P on the bottom of the graphic board covering part of the blue edge 13_P of the orthogonal coordinate. Shows on top the horizontal blue edge 8_12 covering also the red edge 2_4.

Follows the construction of the equations to define the coordinates of point P on the orthogonal system derived from the coordinates of P on the CANMO.
The method called "Trilateration" described in the Wikipedia page was used to obtain equations [5] and [9], to calculate the two first orthogonal coordinates of point 1, as shown on graphical panels 1 to 3 on the animation. In next stage, the orthogonal coordinates of point P are calculated with equations [15], [18] and [21]. The drawings in the animations and in figure-1 are in the same scale. Figure-1 (a) shows three spheres used in "Trilateration", centered on the common plane containing the first and second axes CANMO and the first and second orthogonal axes. It can be seen in figure-1 (a) and (b) the edge 0_2 of length PX. This edge is named a in the deduction of the orthogonal coordinates of point P below. Also the radius of the sphere centered in 0 with length PZ in figure-1 (a) and the edge 0_1 drawn in figure-1 (b) and (c) will be named c. And the edge 0_6 of length PY in figure-1 (a) and (c) willbe named b. The parallel projection of pont P on the plane given by the first and second axes of the orthogonal system in figure-1 (a), Puv, is shown by the red cross. Figure-1 (b) shows how to calculate the length of diagonal f1 and figure-1 (c) shows the calculation of diagonal f2.
 

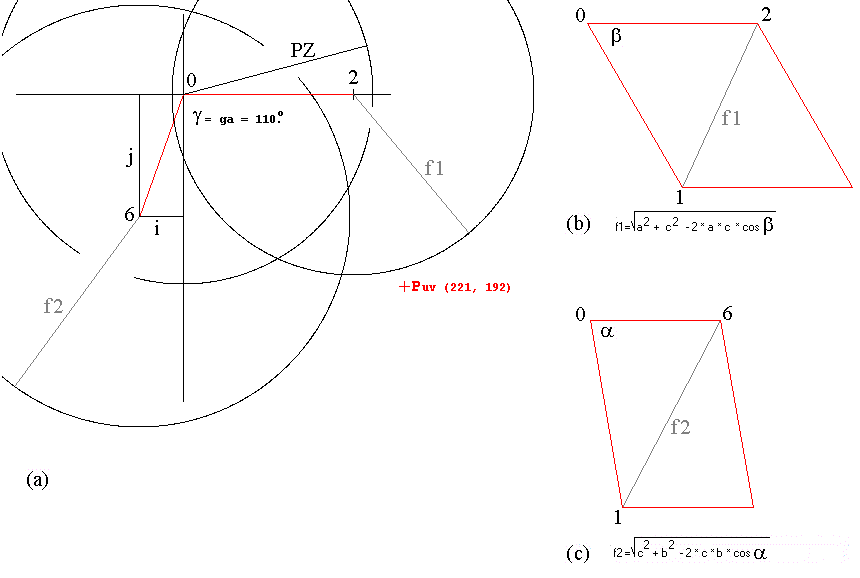
Figure-1. (a) shows the "Trilateration" in the same scale as the animated graphical panels. (b) and (c) shows the calculation of diagonal f1 and f2 in the same scale as the animated graphical panels, respectively. This can be followed in any good basic trigonometry book.

The section below shows  the obtention of the three orthogonal coordinates u, v and w derived from the coordinates of the same point P in the other system. The intersection of the 3 spheres in figure-1 (a) will be calculated from equation [1] to [9] preliminary to convert the first and second coordinates of point 1 of the parallelepiped observed in graphical panels 3 and 8 to the cartesian coordinates of point 1 observed in graphical panels 5 and 10.

Equation [1] is used for the sphere centerd on 0 on figure-1 (a), recall the coordinate PZ is represented by parameter c.

 c² = x² + y² + z²         [1]

The equation for the next sphere is used, centered on 2 on figure-1 (a).

( f1 )² = ( x - a )² + y²  + z²     [2]

And the equation for the third sphere centered on point 6 on figure-1 (a). Distances i and j will be used later, defined by equations [11] and [12].

( f2 )² = ( x - i )² + ( y - j )² + z²      [3]

The following condition will be always valid on the parallelepiped defined by point P on CANMO.

( a - c ) < f1 < ( a + c )     [4]

The obtention of x, [1] - [2]:

x = ( c ² - f1² +  a² ) / ( 2 * a )      [5]

Equation [5] defines the first orthogonal coordinate to point 1, see animated graphical board number 5 and 10.

After substitution of [5] in [1]:

 ( c )²  = {[c² - f1² + a² ]² / 4a² } + y² + z²       [6]

And arrangement of [1]:

y² + z² = c ² - x²        [7]

After substitution of [7] in [3] and simplification:

( f2 )² =( i*2 ) - ( 2 * x * i ) + (2 * j) -( 2 * y * j ) + c²             [8]

After isolating y:

y = [ c² - ( f2 )² + i² + j² - ( 2 * x * i ) ] / (  2 * j )        [9]

Equation [9] defines the second orthogonal coordinate for point 1, see animated graphical board number 5 and 10.

To obtain the first orthogonal coordinate u for point P:

u = a + i + x               [10]

Remember::

i = b * cos             [11]

j = b * sen             [12]

f1 = ( a² + c² - 2 * a * c*cos  )^0.5                       [13]

f2 = (c² + b² - 2 * c * b*cos  )^0.5                       [14]

Definition of the orthogonal coordinate u after substitution of [5] and [11] and [13] in [10] and final simplification:
 

u = a + ( b  * cos ) + ( c * cos )                        [15]

From [15] and [10] it follows:

x = c * cos                [16]

To calculate the second coordinate  v:

v = j + y                [17]

Substitution of  [9] and [11] and [12] and [14] and [16] in [17] to obtaind the second orthogonal coordinate v of point  P:
 

v = ( b  * sen ) + [ c * (cos - cos * cos ) / sen]                      [18]

Development of the third orthogonal coordinate w of point P:

Remember:

Definition of the volume for a completely oblique parallelepiped, see  graphical panel 3 and 8, please note that a=PX, b=PY e c=PZ:

volume =  a * b * c * [1-cos²() - cos²() - cos²() + 2 * cos * cos * cos ]^0.5            [19]

Definition of the area of the base (ab) on a completely oblique parallelepiped:

remember: volume of the parallelepiped can be defined also by the multiplication of the base area by the height

Base area (ab) = a * b * sen                         [20]

The searched third orthogonal coordinate w of point P is exactly the height of the oblique parallelepiped, obtained after the division [19] / [20]:
 

w = { c * [1-cos2() - cos2() - cos2() + 2 * cos * cos * cos ]0.5 }/ sen                           [21]

This procedure was used on the application  GIRA7B.

Exercise

Find the coordinates for the points 0, 1, 2, ...P, ... 7 on CANMO and transfer to the application GIRA7B and identify the projection observed on the graphic board 398. Include a copy of the values for the orthogonal coordinates of point P obtained on the bule page of GIRA7B and write what should be done to find the asked projection, in black and white. Conclude.

Please send your comments.

Table of subjects.

Presentation
Other	Varied	Oblique and orthogonal systems study
		Diary
		Study of the oblique at all coordinate system and the orthogonal coordinate system
		The Great Wall of China and the Great Higway of Love