=
45o about the reference line x and obtain
P1' on plane xy.
Do the same for P1 and P2.
Last Update 24/ 9/ 2014
The 3D computation display on the figure above represents a rotation of vertex P2 of the cube with Cartesian coordinates 5; 10; 10 about the cube diagonal in red that is defined by vertices P0 (5; 0; 0) and P1 (-5; 10; 10). The course of point P2 is shown by a regular sequence of colored disks projected until the 120o rotation is completed. After the rotation angle of 120o is executed P2 will shift to P3 (-5; 10; 0). The Cartesian coordinates along x, y and z for the vertices of the cube are listed in blue on the left side of the figure.
However the computer performs 8 steps to complete the rotation, as explained in the following text.
Consider the following:
x, y, z = Cartesian frame of reference with origin at o.
P0, P1 = Two points used to define the rotation axis coincident with the diagonal of the cube.
P2 = Point to be turned 120o.
Tabel-1.Initial coordinates
| Point | x | y | z |
| P0 | 5 | 0 | 0 |
| P1 | -5 | 10 | 10 |
| P2 | 5 | 10 | 10 |
Step-1. Shift point P0 to the origin
after displacing it -5x; 0y; 0z.
Do the same for P1 and P2.
Table-2.Coordinates obtained after step-1.
| Point | x | y | z |
| P0' | 0 | 0 | 0 |
| P1' | -10 | 10 | 10 |
| P2' | 0 | 10 | 10 |
Step-2. Rotate =
45o about the reference line x and obtain
P1' on plane xy.
Do the same for P1 and P2.
Apply the rotation matrix
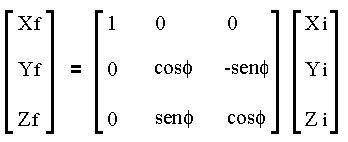
Table-3.Coordinates obtained after step-2.
| Point | x | y | z |
| P0'' | 0 | 0 | 0 |
| P1'' | -10 | 0 | 10 * (21/2) |
| P2'' | 0 | 0 | 10 * (21/2) |
Step-3. Calculate the rotation angle for the line segment oP1'' to bring point P1'' on the reference line z .
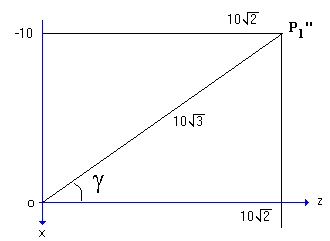
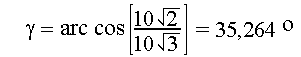
Step-4. Rotate point P1'' and point P2'' 35,264o about the reference line y.
Apply the rotation matrix
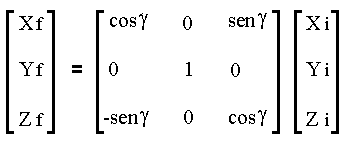
Table-4.Coordinates obtained after step-4.
| Point | x | y | z |
| P0''' | 0 | 0 | 0 |
| P1''' | 0 | 0 | 17,321 |
| P2''' | 8,1650 | 0 | 11,547 |
Step-5. Execute the selected rotation 
= 120o on point P2'''
about the reference line z.
Apply the rotation matrix
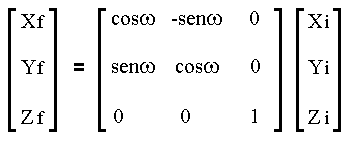
Table-5. Coordinates of point P2iv obtained after
step-5.
| Ponto | x | y | z |
| P2iv | -4,0825 | 7,0711 | 11,547 |
Step-6. Revert: rotate point P2iv -35,264o about the reference line y.
Table-6. Coordinates of point P2v obtained after
step-6.
| Ponto | x | y | z |
| P2v | -9,9999 | 7,0711 | 7,0711 |
Step-7. Revert: rotate point P2v -45o about the reference line x.
Table-7. Coordinates of point P2vi obtained after
step-7.
| Point | x | y | z |
| P2vi | -10 | 10 | 0 |
Step-8. Revert: shift point P2vi displacing it +5x; 0y; 0z to the final position.
Table-8. Coordinates of point P2vii obtained after
step-8.
Rotation done.
| Point | x | y | z |
| P2vii | -5 | 10 | 0 |
Conclusion
Point P2vii and point P3 coincide.
Note
The program of this page was obtained with the help of the resource Rotation of Objects About an Arbitrary Axis.
Exercise
Use the above mentioned resource to obtain the final Cartesian coordinates for initial point P2 ( 5; 10; 10 ) after rotation at first equal to 120o and after rotation equal to -120o and after rotation of 240o about the same axis defined by points P0 (5; 0; 0) and P1 (-5; 10; 10). Write your conclusion. Suggestion: use x[0] = 5; y[0] = 10; z[0] = 10 and x[1] = 5; y[1] = 10; z[1] = 10 because the resource program demands at least two points to define a segment, in this case the segment has length equal zero.
Reference
Fundamentals of Crystallography, Edited by C. GIACOVAZZO, Second Edition, Oxford University Press, Great Britain, 2002.
Please send your comments.
Table of subjects.