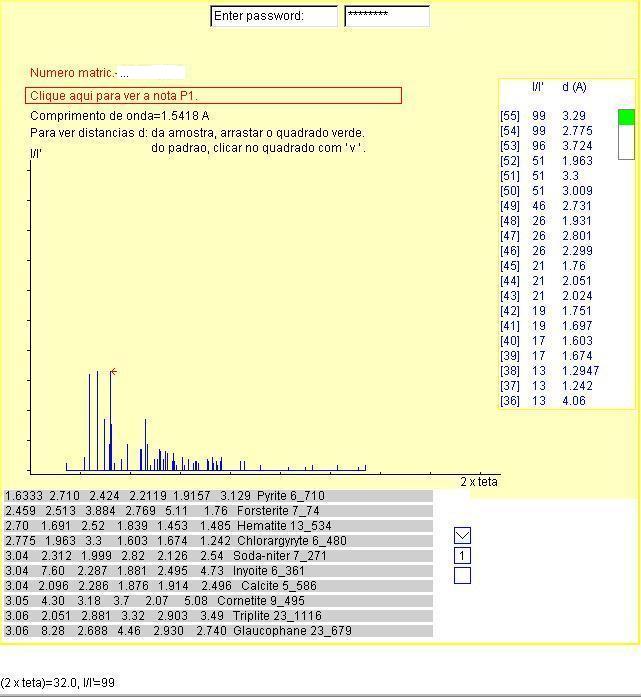
You are invited to use the Hanavalt1 method to identify the sample components through the diffractogram on the figure, in blue. A mouse move action over a diffractogram peak of the sample will show the diffraction angle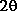
in blue
and the relative intensity in this simulation I = peak height
and background I'=1.
Table-A shows the number of each diffracted ray in brackets in decreasing order of relative intensity I/I' and the distance d in Angstrom (1 A=10-10 m) between crystallographic planes "rich in atoms"2 on the sample3. A mouse drag action on the green square on table-A will show other sections of the table. X-ray with wavelength equal to 1,5418 Angstrom4 was used in this simulation.
Table-B shows six distances d as defined above in decreasing order of relative intensity I/I' for each standard5, respectively on each line on page 1. If one of the 10 standards in the page has d distances matching with the sample, a click on the line will change the line color from gray to red and will display the complete set of d distances of the selected standard on table-C organized as in table-A and will also display the difractogram of the standard in black. A mouse move action over a peak on the standard difractogram will show the angle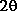
of the
diffracted ray and the relative intensity in black. Click on button V
to see next page of standards, until page 11. To return to the previous
page click on button with inverted V. If there is no standard matching
with the sample in one page it will be necessary to search in another page
on table-B.
A new access to this page Analysis of a Mixture of Minerals - Simulation will present a sample with another different mixture of minerals.
